久赌必输的数学原理
我们先设定一个赌博游戏是绝对公平的。
假设一:每次游戏你都有50%的概率赢1元,有50%的概率输1元。
假设二:你有本金X元,退出机制有两种:1、赢到Y元;2、输到0元(即输光)。
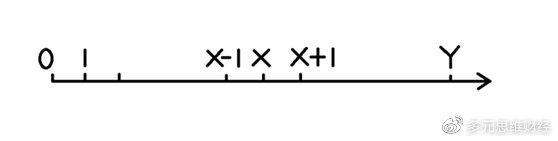
设本金有n元时输光的概率为P(n):
那么根据游戏规则,有50%的概率本金会变成n-1,有50%的概率本金会变成n+1,则
P(n)=0.5*P(n-1)+0.5*P(n+1),等式两边同乘以2,可以整理成下式:
P(n)-P(n-1)=P(n+1)-P(n),即P(n)是一个等差数列。
又因为当你本金为0时,你就已经退场了,所以输光的概率为100%,即P(0)=1;
当你本金为Y时,你因为已经达到目标也退场了,所以输光的概率为0,即P(Y)=0。
所以从0到Y,每一单位本金的概率变化△P=(1-0)/Y。
所以P(X)=1-X/Y=(Y-X)/X,其中(Y-X)是你要赚的钱,而Y是你要达到的钱。
举例说明以上表达式告诉我们的道理:
1、假设你的本金X=100元,你想要赚到120元,那么Y-X=20元,所以你输光的概率就是20/120=1/6,也就是你赢到120元离场的概率为5/6。
2、仍然X=100元,如果你想赚到200元,即翻一倍,此时输光的概率为100/200=50%,同时赢钱离场的概率也为50%。
3、仍然X=100元,假如这次你想赢到1000元,那么你输光的概率=900/1000=90%,而赢钱的概率只有10%。
所以经过以上讨论,我们可以归纳出一个推论,就是Y越大你输光的概率就越大,那么当Y趋近于无穷的时候,你输光的概率就会为100%(P=1-X/Y,其中X/Y趋近于0),而你赢的概率也就是0。这就是所谓的久赌无赢家。
其实这个例子在生活中也非常常见,比如赌徒和赌场老板在进行对赌的过程中,由于赌场的资金量非常的大,即便是在这种非常公平的规则下,赌徒也不可能把赌场搞破产,而只会是反过来赌场把赌徒搞破产;我们在炒股票的时候,假如我们只想赢个10%就离场,那么大概率不会赔光,假如我们是想翻一倍再走,那么就有可能会输光,假如我们再加杠杆加10倍,就会发现有极大的概率会输光本金。
更不要说几乎所有的赌博游戏,你赢的概率都低于50%(赌场有不公平的游戏规则、股市有你不知道的内幕消息、再加上你不可能永远保持理性),再加上大数定律,你赢一把或你赢几把都是可能的,但是你会输光却是一定的。
究其原因,其实就像渔夫和金鱼的故事,我们不是输给了别人,而是输给了自己的贪婪。人越贪婪就越有可能输光自己。